top of page
Polynomial Functions Reflection Activity
 

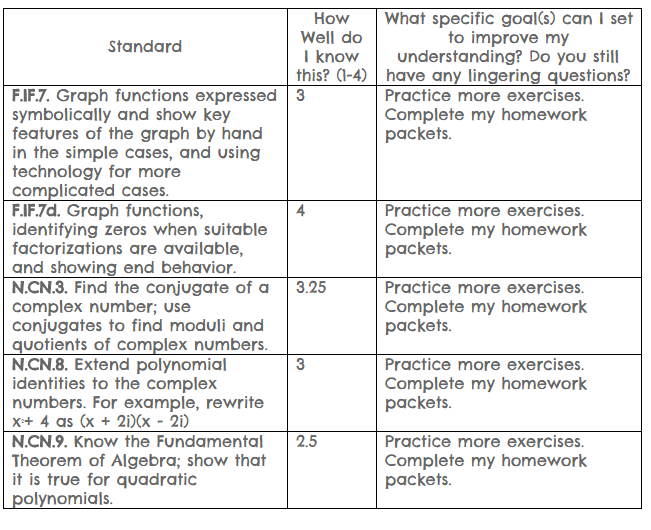
Common Core Standards

F.IF.7. Graph functions expressed symbolically and show key features of the graph by hand in the simple cases, and using technology for more complicated cases.

F.IF.7d. Graph functions, identifying zeros when suitable factorizations are available, and showing end behavior.

N.CN.3. Find the conjugate of a complex number; use conjugates to find moduli and quotients of complex numbers.

N.CN.8. Extend polynomial identities to the complex numbers. For example, rewrite x2+ 4 as (x + 2i)(x - 2i)

N.CN.9. Know the Fundamental Theorem of Algebra; show that it is true for quadratic polynomials.
 
Formative Assessments
Daily Work in Packets: 3
Homework: 2
Solving Polynomial Equations and Inequalities Quiz: 3.5
 
Summative Assessments
Polynomials Mid Unit Test: 3
Polynomials End of Unit Test: 3.5
 
Given the numerical, algebraic, and graphical representations of the polynomial functions below, state as many facts as you possibly can about each of the three different functions. As you do this, reflect upon the standards covered in the Polynomial Functions Unit and form a plan on how you can improve.

  • It’s quartic because the table shows three zeros, and one of them has a multiplicity of 2. Thus the graph is to the fourth degree, which means it is a quartic function.

  • Both ends rise: as x approaches negative infinity, g(x) approaches infinity. This means the function has a positive leading coefficient.

  • The y-intercept is 2.

  • The graph crosses the x-axis at -1, 2, and somewhere between 0 and 1.

  • It has 2 points of inflection.
     
     
     
     
     
     
     
     
     

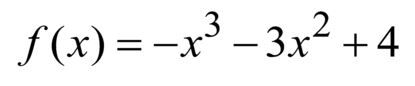
  • It is a cubic function, because the highest degree is 3.

  • It has a negative leading coefficient. This means that as x approaches negative infinity, f(x) approaches infinity, and as x approaches infinity, f(x) approaches negative infinity.

  • The y-intercept is 4.

  • 1 point of inflection.
     
     
     
     
     
     
     
     
     

Graph of h(x)

 

  • It’s a quartic function: it touches/crosses the x-axis 3 times, yet at x=-4, it has a multiplicity of 2, so it has 4 zeros.

  • The leading coefficient is positive, both ends of the line are rising.

  • Y-intercept: somewhere between 2.5 and 3

  • Zeros: -4, 1, 3.

  • 2 points of inflection.

Student Improvement Plan
bottom of page